John Horton Conway: The Mathematician Who Made Math Fun
By Helen Wong 王思齊
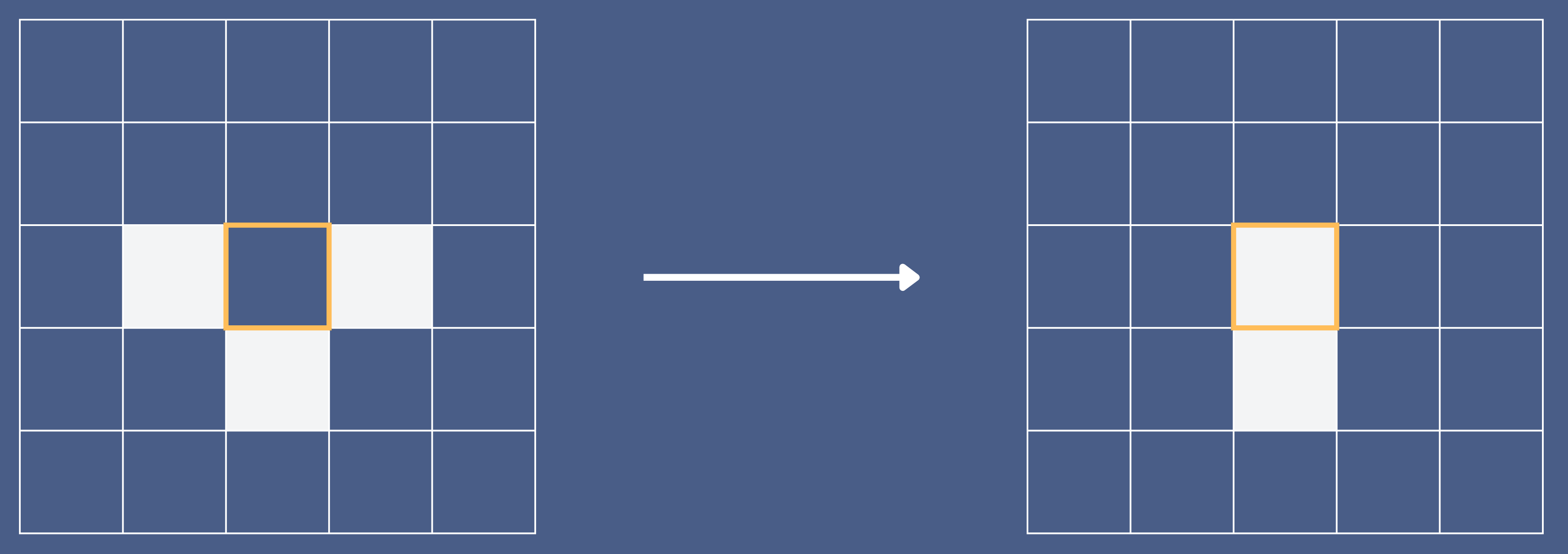
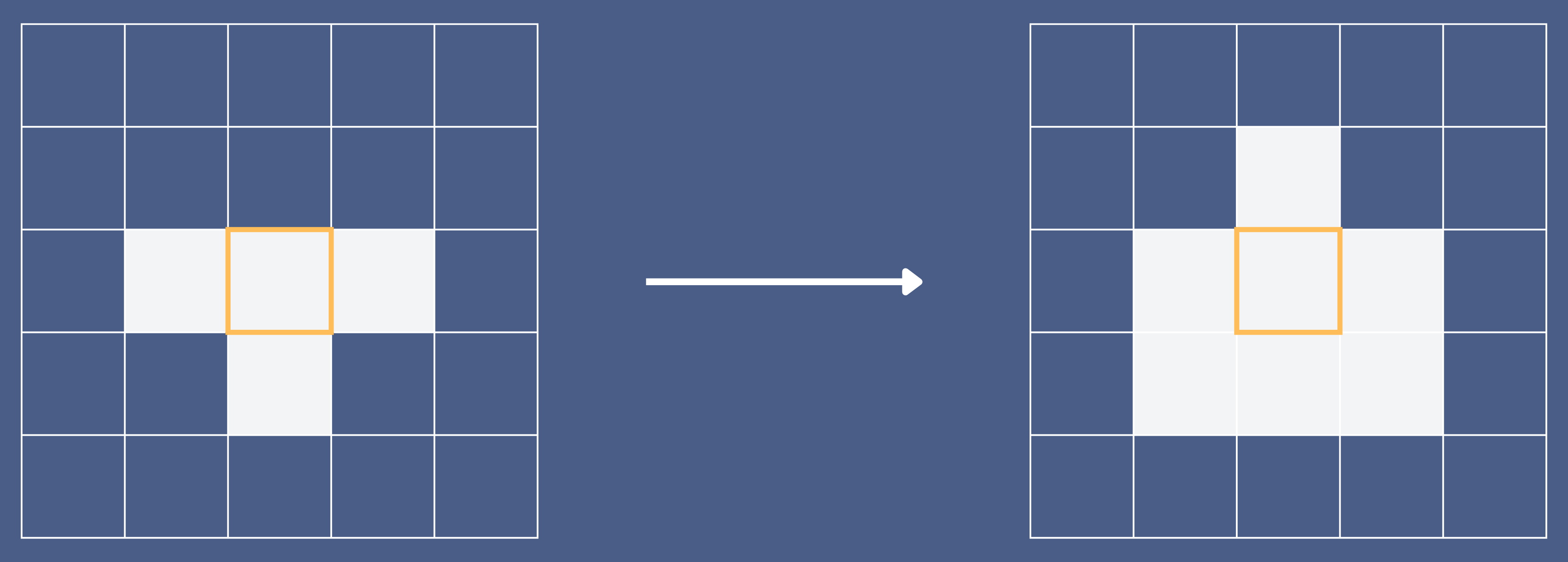
Quiz time: Can you recognize the following pattern?

The Game of Life
If you are an avid fan of the Game of Life, you will immediately identify this as the famous Gosper glider gun. However, for those new to the game, you might be surprised to learn that this lifelike animated pattern – a gun periodically firing a stream of gliders – is built upon a deceptively straightforward set of rules [1] (Table 1). The player can start the game by specifying a “seed pattern,” which will “evolve” in each round (or “generation”) based on the rules. Some hardcore fans have classified the output and created a lexicon with all the special “life forms.”
|
Birth: A dead cell becomes alive when it has three live neighbors.
|
|
Survival: A live cell survives when it has two or three live neighbors.
|
|
Death (underpopulation): A live cell dies when it has one or no live neighbors.
|
|
Death (overpopulation): A live cell dies when it has four or more live neighbors.
|
Table 1 The four rules of the Game of Life [1]. Each cell has eight neighbors. Shaded cells are alive while empty cells are dead.
John Horton Conway
For over half a century, the Game of Life has fascinated countless mathematicians, computer scientists, and hobbyists with its infinite possibilities. And its creator, British mathematician John Horton Conway (1937–2020), lived a life just as full of wonder and playfulness.
Born in Liverpool in 1937, Conway’s career followed a familiar path of some of the greatest mathematicians of his time: He became interested in mathematics at an early age, went on to study mathematics at the University of Cambridge and received his doctorate there in 1964, then stayed on as a faculty member until moving to Princeton University in 1986 [2, 3].
Yet, on the other hand, Conway was very much an atypical academic [3, 4]. Instead of being confined to his office at Princeton, he enjoyed roaming around the departmental common room and the hallways of the mathematics building. As a teacher, he often brought pocket props (such as ropes, cards, dice, Slinkys, and even a toy bike!) to his classes and would sometimes even “throw a shoe at the window if he thought the students were asleep [4].” Perhaps most famously, he approached mathematics with games and puzzles.
“I learned very quickly that playing games and working on mathematics were closely intertwined activities for him [John Conway], if not actually the same activity.”
— Manjul Bhargava, Professor of Mathematics at Princeton University [3]
Doomsday Algorithm
Here's yet another mathematical trick invented by Conway that you will not only enjoy but also find useful: the Doomsday Algorithm [5]. By working out the “doomsdays,” or a set of easily memorable dates that always fall on the same day of the week in the same year (Table 2), you can quickly determine the day of the week for any given date. Before delving into how the algorithm works, let’s first clarify what we mean by the term “doomsday.” Here, doomsday is defined as the day of the week for any doomsday dates in a year.
Let’s start from a basic fact – the doomsday of 2000 was Tuesday. Conceptually, by observing how the doomsday shifts across years and centuries, one can work out the doomsday of any year. We can then find the day of the week of a particular date by calculating the difference between the date and its nearest doomsday date.
| Month | January | February | March | April | May | June |
| Doomsday | 3/1 (or 4/1 on a leap year) | 28/2 (or 29/2 on a leap year) | 14/3 | 4/4 | 9/5 | 6/6 |
| Month | July | August | September | October | November | December |
| Doomsday | 11/7 | 8/8 | 5/9 | 10/10 | 7/11 | 12/12 |
Table 2 A set of easily memorable doomsday that always fall on the same day of the week. (Can you spot some patterns? Any important date for the hungry mathematicians?)
Still confused? Let’s go over a simple example together [5]. Here’s a tip: You can always refer to the cheat sheet at the end of the article for quick reference to any “unfamiliar numbers” you find in the next paragraph.
Suppose we want to know the day of the week for December 26, 1937 (Guess what? It’s Conway’s birthday! [2]). First, let’s start from year 1900. The century code for the 1900s is 3, meaning that the doomsday of 1900 was Wednesday. Here’s a fact: The day of the week of the same date moves forward by one day in the next year, and by two days for a leap year. Conway has, again, analyzed the pattern of the results and developed a “year shortcut.” For the year 1936, we can add the year shortcut 3 to the century code, so 3 + 3 = 6. The doomsday of 1936 was Saturday. Then we may safely arrive at the conclusion that the doomsday of 1937 was Sunday, as there was no leap day after December 26, 1936 until the date of interest.
The nearest doomsday date to December 26 is December 12, so we subtract 12 from 26 to get 14. Dividing 14 by 7 gives us a remainder of 0, meaning that December 26 falls on the same day of the week as the doomsday of 1937, i.e. Sunday.
Voila! We now know that Conway was born on a Sunday.
While most may only use this as a party trick, Conway took it to another level. He challenged himself to calculate ten random dates to log on to his computer and set a goal of doubling his speed every five years [6]. His record was an impressive 15.92 seconds!
Audioactive Sequences
By now, some of you may recall that we previously covered another piece of Conway’s recreational mathematics work in Issue 023: audioactive sequences, in which the next term in a series is generated by reading aloud the preceding term (Footnote 1). Conway discovered some intriguing properties of these sequences and described them with chemistry jargon, but we won't delve into that here to avoid spoilers for those who have not read the article.
“Serious Mathematics”
Although Conway’s name is often associated with mathematical games and puzzles, most notably the Game of Life, it would be unjust to overlook his significant contribution to numerous branches of “serious mathematics” including group theory, higher-dimensional geometry, tessellations, knot theory, number theory, abstract algebra, mathematical logic and analysis [7]. In fact, Conway himself considered his invention of the “surreal numbers” to be his greatest achievement [3, 4]. This new number system encompasses all real numbers, including integers, fractions, and irrational numbers, as well as “infinitely small” and “infinitely large” numbers. As was often the case, Conway's inspiration for the surreal numbers came from his contemplation of the rules of a game. It was the game of Go on this occasion.
Concluding Remark
Whether it was to the mathematical community, game enthusiasts worldwide, or the Princeton campus, Conway's passing due to COVID-19 complications in 2020 was a great loss. Nonetheless, his spirit of viewing mathematics as a form of play continues to inspire. This enduring legacy is perhaps best exemplified by the recent discovery in the Game of Life of the two long missing repeating patterns that repeat itself after 19 and 41 “generations” respectively [1].
|
Conway’s Game of Life |
The Number Sequence That Needs to Be Said (Issue 023) |
|
https://sciencefocus.hkust.edu.hk/the-number-sequence-that-needs-to-be-said |
Cheat Sheet of the Doomsday Algorithm
| The day of a week | Sunday | Monday | Tuesday | Wednesday |
| Code | 0 | 1 | 2 | 3 |
| The day of a week | Thursday | Friday | Saturday | |
| Code | 4 | 5 | 6 |
Table 3a Numerical representation of the days of a week.
| Year | 1700 | 1800 | 1900 | 2000 |
| The day of a week of the doomsdays | Sunday (0) | Friday (5) | Wednesday (3) | Tuesday (2) |
| Year | 2100 | 2200 | 2300 | 2400 |
| The day of a week of the doomsdays | Sunday (0) | Friday (5) | Wednesday (3) | Tuesday (2) |
Table 3b Century code from the year 1700 to 2400. In fact, the century code "0, 5, 3, 2, ..." repeats every four centuries. In other words, any two centuries share the same code if they differ by a multiple of 400 years.
| The last two digits of the year | 00 | 12 | 24 | 36 | 48 |
| Value | 0 | 1 | 2 | 3 | 4 |
| The last two digits of the year | 60 | 72 | 84 | 96 | |
| Value | 5 | 6 | 7 | 8 |
Table 3c Year shortcut.
1 Editor’s note: For example, the sequence 1, 11, 21, 1211, … is an audioactive sequence which can be read as “one 1, two 1’s, one 2 one 1, …” Similar to the Game of Life, Conway and math lovers seriously investigated the pattern of numbers emerged from the puzzle.
References
[1] Stone, A. (2024, January 18). Math’s “Game of Life” reveals long-sought repeating patterns. Quanta Magazine. https://www.quantamagazine.org/maths-game-of-life-reveals-long-sought-repeating-patterns-20240118
[2] Curtis, R. T. (2021). John Horton Conway. 26 December 1937—11 April 2020. Biographical Memoirs of Fellows of the Royal Society, 72, 117–138. https://doi.org/10.1098/rsbm.2021.0034
[3] Zandonella, C. (2020, April 14). Mathematician John Horton Conway, a “Magical genius” known for inventing the “Game of Life,” dies at age 82. Princeton University. https://www.princeton.edu/news/2020/04/14/mathematician-john-horton-conway-magical-genius-known-inventing-game-life-dies-age
[4] Landau, E. (2020, April 20). Remembering mathematical magician John Conway. Scientific American. https://www.scientificamerican.com/blog/observations/remembering-mathematical-magician-john-conway/
[5] Numberphile. (2021, October 31). The Doomsday Algorithm – Numberphile [Video]. Youtube. https://www.youtube.com/watch?v=z2x3SSBVGJU
[6] Roberts, S. (2015, July 28). John Horton Conway: The world’s most charismatic mathematician. The Guardian. https://www.theguardian.com/science/2015/jul/23/john-horton-conway-the-most-charismatic-mathematician-in-the-world
[7] Mutalik, P. (2020, October 15). Celebrating the playful magic of John Horton Conway. Quanta Magazine. https://www.quantamagazine.org/three-math-puzzles-inspired-by-john-horton-conway-20201015/
_bg.png)
_bg.png)