Will Mathematicians Be Replaced? – Computers in Mathematics
By Sonia Choy 蔡蒨珩

Could a computer do math?
Well, you may think, of course it can – you only need to type “1 + 1” into the Google search bar for it to show the number two. Computers, in fact, were built to do math; the name comes from the root “compute”, and was formerly used to refer to actual people who do calculations by hand before we had computers. Indeed, by using Microsoft Excel or programming languages such as Python or C++, a computer can do plenty of difficult calculations far faster than a human being could. But mathematicians are far more interested in another type of math – proof writing.
Consider the following problem: Start with any number. If it is even, divide the number by two. If it is odd, multiply it by three, then add one. Does this sequence always get to 1 eventually? This innocent-looking problem is known as the Collatz conjecture, and remains unsolved to this day. A computer could check whether this is true for an arbitrarily large number (given enough time and computing power), but to prove that it goes to 1 for any number takes far more effort and new techniques; we do not know how to do it yet.
Consider another problem that we can solve. Given the quadrilateral in Figure 1, how do you find the highlighted angle? Well, we apply the theorem “exterior angle of cyclic quadrilateral” to prove that the two are the same. Could a computer do the same thing? If we teach it the theorem, then yes. Can computers, then, prove things that we do not yet know?
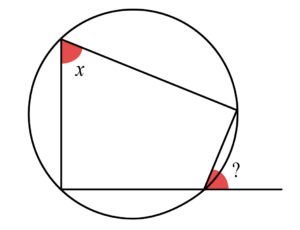
Figure 1 Exterior angle of a cyclic quadrilateral.
Well, maybe. We need to teach a computer how to do mathematics.
The first task is to formalize the mathematics we know now. One recent contender for this is Lean, a software developed by Microsoft engineer Leonardo de Moura in 2013 [1]. Big swathes of basic university-level mathematics have been formalized (rewritten in a way a computer understands) since its foundation, and there are multiple ongoing efforts to build up a bigger mathematical library for Lean that it can draw on.
To get a taste of how this is done, there is a game available online called The Natural Number Game [2]. There you can try teaching a computer to count and do basic addition and multiplication – even the most basic facts, like “the natural number after x is x + 1,” are things we need to tell the computer.
Being able to count is, of course, a long way from what current research in mathematics looks like. But Lean can be fed more and more complex theorems which allow it to do far more: At the end of 2020, mathematician Peter Scholze had doubts about parts of a proof he wrote. Scholze, a Fields Medalist (footnote 1), works in arithmetic geometry, a field known for being extremely technical and abstract; he and Dustin Clausen had proved a fundamental statement to the field a few years ago, but there were parts of it he was unsure about – and who better to check it than a machine? Hence began the Liquid Tensor Experiment, an attempt to verify their proof using Lean [3].
Six months later, the results were positive – their proof was correct, albeit with a few slight imprecisions. A group of mathematicians, with the vast majority of work done by Johan Commelin, were able to follow their written out proof and “teach” it to a computer, hence verifying their proof [4].
So it is actually possible that a computer could actively participate in research-level mathematics – with a slight catch. Here Lean is a proof assistant, not a proof generator; the computer’s checking of the proof relies on the human effort of formalizing the proof, since it cannot read and digest human prose by itself. It also certainly cannot come up with a proof of this very technical statement all on its own; while Lean can make simplifications that might not come as completely obvious to humans, it still follows the skeleton of the argument given by Scholze and Clausen and merely checks whether it is logically correct.
There is also another dimension to this problem; research in mathematics is largely about proving statements, but part of it is also about choosing and proving the “right” statements. Often when mathematicians cannot prove a certain statement, they go about proving a simpler version that is still “interesting”. These words, however, are much more difficult to define than absolute concepts like true and false; for example, while we might not yet have enough machinery to prove the Twin Prime Conjecture (i.e. “there are infinitely many pairs of primes that have a difference of two”), we are able to prove a weaker version of this statement, that there are infinitely many pairs of primes with a difference less than or equal to 246 [5], and notably this weaker version is still of interest to us.
To look for ways to simplify a given conjecture into the right statement is straightforward to a human being, but not necessarily easy to a computer. There are ongoing efforts to study the difference between “easy” and “hard” problems by using machine learning, such as a recent effort began by Timothy Gowers [6]; once this barrier is cleared, we might have more progress in getting computers to prove “not-too-hard” statements that are “useful” to mathematicians.
We are, also, still a long way away from solving problems that need some sort of “cheat” or “hint”, or involve constructing certain examples; these problems are often extremely difficult by brute force searching but are almost trivial once you know what method you need. Without a human feeding the hint to the prover, at present it is impossible for a computer to come up with the “hint” itself, and even for a mathematician, it takes years of training to be able to spot the best way to attack a problem.
But recently, AIs have also been able to solve harder problems independently – it is now possible for certain engines (ROBOT [6], Lean [7]) to solve “routine” undergraduate-level math problems, as well as problems from the International Mathematical Olympiad, a worldwide competition for high schoolers often called the Olympics of Mathematics. So it is only natural to expect that computers will be able to solve harder and harder problems in the future – perhaps, at some point, even surpassing human capabilities.
So what role will computers play in research-level mathematics in the future? The honest answer is that nobody knows; AI-optimists will claim that computers will eventually replace mathematicians, in the time frame of ten years to a century; those less optimistic will claim that mathematicians are irreplaceable. As an aspiring research mathematician, I surely hope that we will not be replaced in the near future (very unlikely). But it is also exciting to see progress both in improving the knowledge base which software can draw from, and in computers’ ability to solve problems hands-on. Perhaps one day they will replace mathematicians – who knows? But first there will surely be a time when computers will aid mathematicians greatly in their research, when they gain the ability to prove tedious statements that nobody wanted to do.
1 Fields Medal: Regarded as the “Nobel Prize in mathematics” (which does not exist), it is one of the most prestigious prizes in mathematics, which is awarded to two to four outstanding mathematicians under the age of 40 every four years.
References:
[1] Hartnett, K. (2020, September 21). At the Math Olympiad, Computers Prepare to Go for the Gold. Quanta Magazine. Retrieved from https://www.quantamagazine.org/at-the-international-mathematical-olympiad-artificial-intelligence-prepares-to-go-for-the-gold-20200921/
[2] Buzzard, K., & Pedramfar, M. (n.d.). Natural Number Game. Retrieved from https://www.ma.imperial.ac.uk/~buzzard/xena/natural_number_game/
[3] Scholze, P. (2020, December 5). Liquid tensor experiment [Web log post]. Retrieved from https://xenaproject.wordpress.com/2020/12/05/liquid-tensor-experiment/
[4] Scholze, P. (2021, June 5). Half a year of the liquid tensor experiment: Amazing Developments [Web log post]. Retrieved from https://xenaproject.wordpress.com/2021/06/05/half-a-year-of-the-liquid-tensor-experiment-amazing-developments/
[5] Polymath, D. H. J. (2014). Variants of the Selberg sieve, and bounded intervals containing many primes. Research in the Mathematical Sciences, 1. doi:10.1186/s40687-014-0012-7
[6] Gowers, W. T. (2022, April 28). Announcing an automatic theorem proving project [Web log post]. Retrieved from https://gowers.wordpress.com/2022/04/28/announcing-an-automatic-theorem-proving-project/
[7] Polu, S., Han, M. J., & Sutskever, I. (2022, February 2). Solving (Some) Formal Math Olympiad Problems. Retrieved from https://openai.com/blog/formal-math/