數學家會被取代嗎?— 電腦在數學中的角色
By Sonia Choy 蔡蒨珩

電腦能從事數學工作嗎?
聽到這個問題的時候,你的第一個反應必定是「可以」吧,畢竟我們只需在Google搜尋「1 + 1」,它就會自動顯示答案「2」。事實上最初發明電腦的目的真的是為了計算;英文名稱「computer」(計算機)來自字根「compute」(計算),在沒有電腦的年代指從事計算工作的計算員。透過微軟Excel或Python及C++等程式語言,電腦的確可以迅速地進行複雜的計算工作,所需時間遠比人類短,可是數學家感興趣的卻是另一種「數學」:寫數學證明。
考慮以下的問題:任意選一個數字作起點,如果這個數字是雙數,把它除以二;如果是單數,先將數字乘以三,再加上一。重覆以上步驟,到底數列最終是不是永遠都會得出1?這個看似簡單的問題就是考拉茲猜想 (Collatz Conjecture),但現在還沒有人能夠解答。電腦可以檢查一個任意大的數字最後會得出甚麼(假設有足夠的時間和計算能力給電腦去計算),但這與要證明任何一個數字最後都會得出1還有一段距離,要解決這個問題肯定需要一些新方法,但擁有電腦的我們卻一籌莫展。
那有甚麼問題是我們可以用電腦解決的呢?例如這道:試找出圖一四邊形中所示的角度。我們都懂得用「圓內接四邊形外角」這條定理去證明兩者相等。那麼,電腦又懂得這樣做嗎?如果我們教曉電腦用這條定理的話,那沒問題;然而,電腦又能不能解開人類還沒解開的數學問題呢?
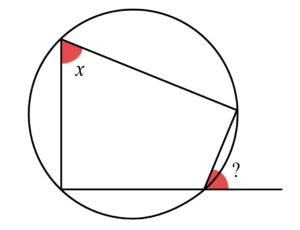
圖一 圓內接四邊形外角
嗯,也許可以吧。但我們要先給電腦上一課數學課。
第一個任務是把我們現在知道的數學知識形式化(formalize)。近年這方面有一個在2013年由微軟工程師Leonardo de Moura開發,叫Lean的軟件 [1]。自Lean問世而來很多大學程度的基本數學知識都已經被形式化(以電腦能理解的形式改寫),現時多方仍在努力豐富Lean的數學知識庫,令其可以引用更多數學知識和定理。
網上有一個叫《The Natural Number》的遊戲讓玩家可以體驗把數學知識形式化的過程 [2]。在遊戲中你可以嘗試教電腦數算、基本加法和乘法,但在這之前你需要告訴電腦例如「x的下一個自然數是x + 1」等最基本的知識。
當然,現時數學家研究的課題遠比數算難,但我們可以對Lean輸入更多更複雜的定理讓其發揮更多。2020年末,數學家Peter Scholze對自己寫的一部分證明有所懷疑;他是菲爾茲獎得主(註一),主要研究以極其專門和抽象見稱的算術幾何。事源他和Dustin Clausen幾年前證明了一條對該範疇非常重要的定理,但他對當中一些細節並不確定。如果要檢查這份證明,還有比電腦更適合的「人選」嗎?於是他們展開了液體張量實驗(Liquid Tensor Experiment),嘗試用Lean來驗證證明 [3]。
六個月後,Scholze和Clausen得到了正面的結果:儘管他們的證明有幾個小漏洞,但大致正確。實驗中,以Johan Commelin貢獻最多的一組數學家在理解Scholze和Clausen寫的證明後,以電腦明白的語言「教」電腦讀懂證明,使其能驗證證明 [4]。
因此電腦的確有能力參與數學研究並作出貢獻,但有一個細節必須注意:上文提到的Lean只能輔助我們檢查證明,但它並不能憑空寫出證明。由於電腦不能讀懂用我們文字寫的證明,因此即使要驗證也要靠我們把證明形式化。電腦亦肯定不能自行創造出這類極為複雜的證明,儘管Lean能洞察到證明中可以作出簡化的地方,並在這些對我們來說未必太明顯的位置精簡證明,但總的來說它還是僅僅順著Scholze和Clausen所寫的論證來檢查證明是否邏輯上正確。
這延伸出另一方面的問題:雖然數學研究大多都是關於證明敘述,但當中亦涉及如何找「正確」的敘述來證明。當數學家不能證明某個敘述時,他們往往會將敘述簡化,先證明比較簡單但仍然「有用」的版本。然而判別何謂「正確」和「有用」並不像分辨對錯那樣非黑即白,這需要用到更高階的思維,譬如我們現在並不能證明孿生質數猜想(其敘述為「前後兩者相差為2的質數對有無限多對」),但是我們卻能退而求其次,證明前後兩者相差少於或等於246的質數對有無限多對 [5],這個安慰獎對我們來說還是有用的。
把猜想簡化成仍然有用的敘述對人類來說並不難,但對電腦來說可能一點也不容易。數學家正嘗試用機器學習(machine learning)研究一個問題到底何謂「簡單」和「困難」,例如Timothy Gowers最近就正著手處理這個問題 [6]。一旦有所突破,也許我們就能讓電腦自行找出一些「不太困難」但仍對數學家有用的敘述來證明。
對於要用上一些「捷徑」或「提示」,或是要建構特別例子才能解決的數學問題,電腦還是鞭長莫及。這些問題通常很難透過蠻力搜尋(brute force searching)以窮舉的方式解決,但當你知道所需的方法後一切卻會迎刃而解。如果沒有人對電腦輸入這個「提示」,現今的電腦是不能自己洞察到的;儘管是數學家,這種直覺也是讀書和實戰多年後的成果。
可是近年人工智能也開始能獨自解決一些較難的問題:一些程式(ROBOT [6] 和Lean [7] 等)都能解開大學本科課程中比較簡單的數學問題,以及高中數學比賽國際數學奧林匹克 (International Mathematical Olympiad) 的試題,因此不難想像電腦在未來將可以解決越來越難的問題 — 也許有一天,它的解題能力甚至會超越人類。
那麼電腦未來在數學研究上會擔任什麼角色呢?說真的,沒有人知道。對人工智能前景樂觀的人會認為電腦數十年或一個世紀內將超越並取代數學家;沒那麼樂觀的人會認為數學家是不可取替的。筆者作為一個希望成為數學家的學生,當然希望我們在短期內不會被電腦取代(其實也不太可能會被取代),但也樂見這些輔助軟件的知識庫變得越來越豐富,電腦的解題能力又不斷在進步。也許電腦真的有一天會取代人類,誰知道?但在這天來臨之前,電腦或許會先掌握書寫數學證明的能力,屆時沒有人想花時間解決的繁複證明工作將得以解決,數學界也必定會經歷一段黃金時期,那時電腦將會成為數學家的得力助手。
1 菲爾茲獎:被喻為「諾貝爾數學獎」(這個獎項並不存在),它是數學界其中一個最崇高的獎項,每四年頒發一次予二至四位年齡為40歲以下的傑出數學家。
參考資料:
[1] Hartnett, K. (2020, September 21). At the Math Olympiad, Computers Prepare to Go for the Gold. Quanta Magazine. Retrieved from https://www.quantamagazine.org/at-the-international-mathematical-olympiad-artificial-intelligence-prepares-to-go-for-the-gold-20200921/
[2] Buzzard, K., & Pedramfar, M. (n.d.). Natural Number Game. Retrieved from https://www.ma.imperial.ac.uk/~buzzard/xena/natural_number_game/
[3] Scholze, P. (2020, December 5). Liquid tensor experiment [Web log post]. Retrieved from https://xenaproject.wordpress.com/2020/12/05/liquid-tensor-experiment/
[4] Scholze, P. (2021, June 5). Half a year of the liquid tensor experiment: Amazing Developments [Web log post]. Retrieved from https://xenaproject.wordpress.com/2021/06/05/half-a-year-of-the-liquid-tensor-experiment-amazing-developments/
[5] Polymath, D. H. J. (2014). Variants of the Selberg sieve, and bounded intervals containing many primes. Research in the Mathematical Sciences, 1. doi:10.1186/s40687-014-0012-7
[6] Gowers, W. T. (2022, April 28). Announcing an automatic theorem proving project [Web log post]. Retrieved from https://gowers.wordpress.com/2022/04/28/announcing-an-automatic-theorem-proving-project/
[7] Polu, S., Han, M. J., & Sutskever, I. (2022, February 2). Solving (Some) Formal Math Olympiad Problems. Retrieved from https://openai.com/blog/formal-math/