How to Eat a Pizza Slice Properly?
By Devandhira Wijaya Wangsa

The Pizza Tragedy
If you were to eat a pizza slice right now, how would you do it? Typically, it goes as such:
- You grab a slice of pizza by its crust.
- The pizza droops and dangles on your hand.
- The topping falls on the table, and you sit in despair as you struggle with the mess!
For centuries since its invention, this is how pizza is tragically eaten. However, if you bend the crust to vertically fold the pizza into half, it can be held straight and easily eaten. I call this the “Gaussian hold,” inspired by the mathematician Carl Friedrich Gauss!
The secret behind this trick – in the mathematical point of view – relates to a concept called curvature. The idea of curvature is not that foreign to us; it is simply a value measuring how “curved” or “bent” something is. For a one-dimensional curve, the more curved it is at a certain point, the greater its curvature. To give a numerical sense, a circle of radius r has curvature 1/r everywhere, so a large circle is “less curved” than a small circle. It is also natural to say that any point on a straight line has no curvature, i.e. zero curvature. Note that it is more accurate to describe the curvature at a certain point, because a curve can have different curvatures at different points.
Nevertheless, in our original question, we are dealing with a surface (well, strictly speaking, a pizza is not exactly a surface because it has thickness, but we can view it as one). So how does the concept of curvature relate to the laws of bending surfaces? The answer relies on a remarkable result related to a specific kind of curvature called the Gaussian curvature.
Enter the Gaussian Curvature
Let’s discuss how we describe the curvature of a surface. Think about the surface of a three-dimensional object such as a piece of paper, a ball, a cylinder, a pringle chip, or even a donut. For a certain point on the surface, notice that you will get a different curvature depending on the orientation of the surface you are considering. To get a more concrete example, take a look at the surface in figure 1 and find the curvature at the center (origin) of the graph.
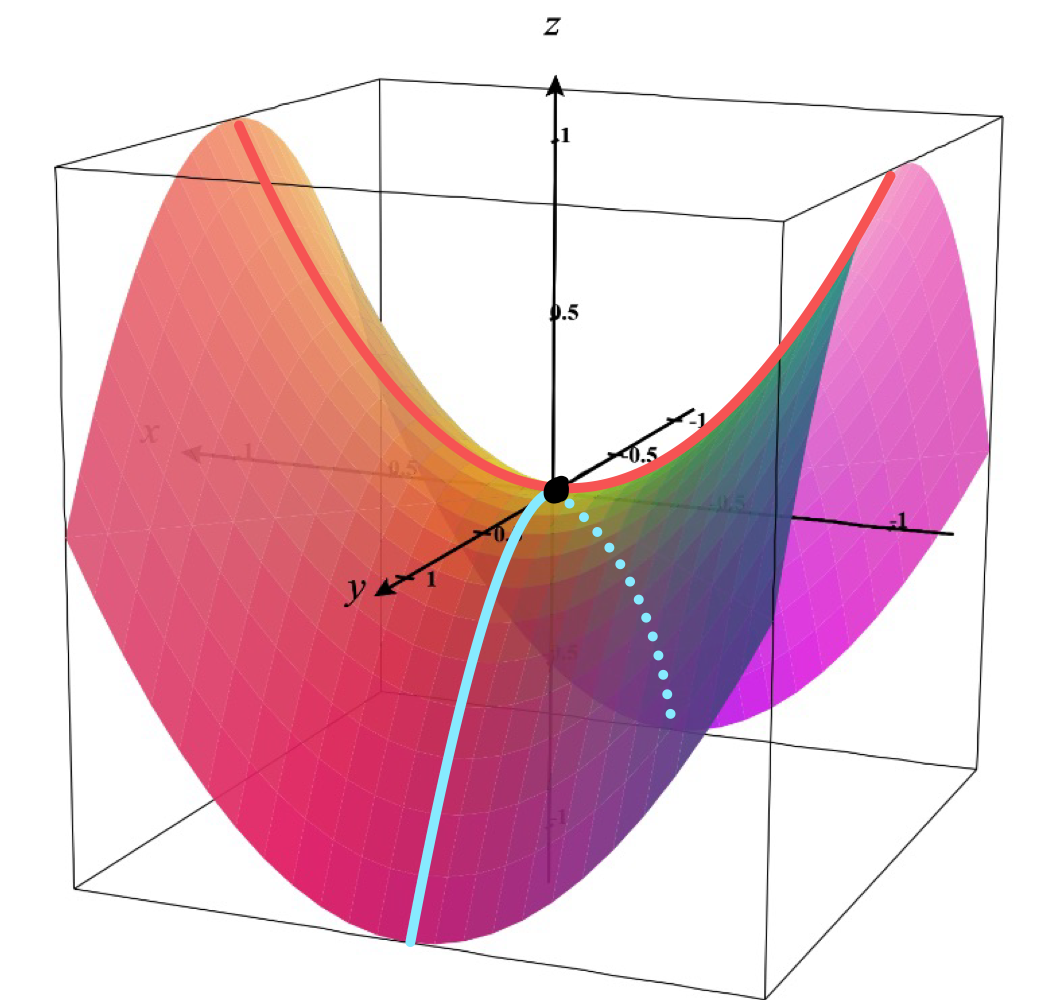
Figure 1 A surface with both a positive (red) and a negative (blue) normal curvature at the center (origin) (footnote 1).
Depending on which orientation of the surface we take (red or blue), we have a different curvature with the red curve going upward on both sides, while the blue curve going downward on both sides. In this case, at the center point, we can say the red curve has a positive curvature, whereas the blue curve has a negative curvature (the definition of positive and negative curvature depends on the convention we use). Note that even though the curves span across the surface, we are considering only the curvature at the center point.
We call this the “normal curvature” – the curvature at a certain point on the surface with respect to a curve passing through the point (footnote 2); in our example, the surface has a positive normal curvature with respect to the direction of the red curve, and a negative normal curvature with respect to that of the blue curve.
Now imagine we take all possible normal curvatures at a point by drawing every curve with respect to all possible directions. From all such possibilities, there has to be the greatest normal curvature and the least normal curvature (footnote 3), multiplying these two curvatures gives the Gaussian curvature.
Let’s look at the three examples in figure 2. The first surface has a positive Gaussian curvature at the labelled point because both the maximum and minimum normal curvatures are positive, hence their product is also positive. The other two shapes have zero and negative Gaussian curvature respectively for the same reasoning. While there are other ways to describe the curvature of a surface at a point, such as mean curvature, Gaussian curvature is the way relevant to our question.
(a) 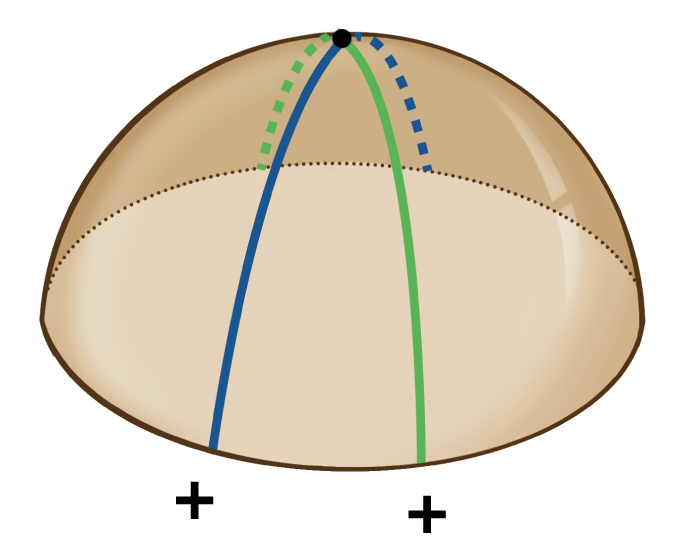 | (b) 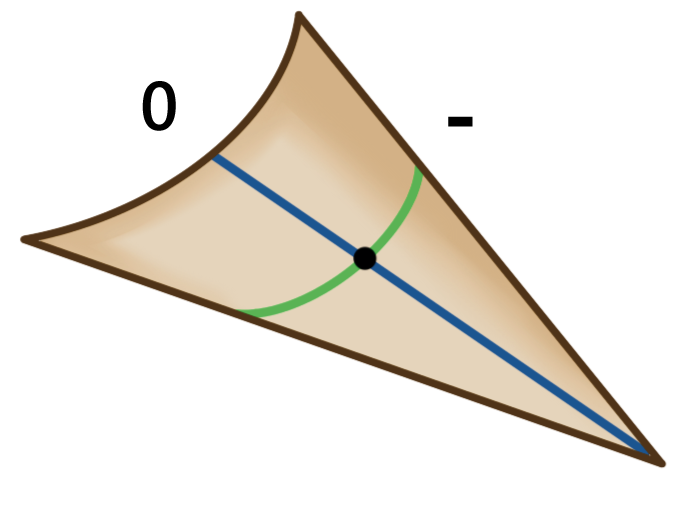 | (c) 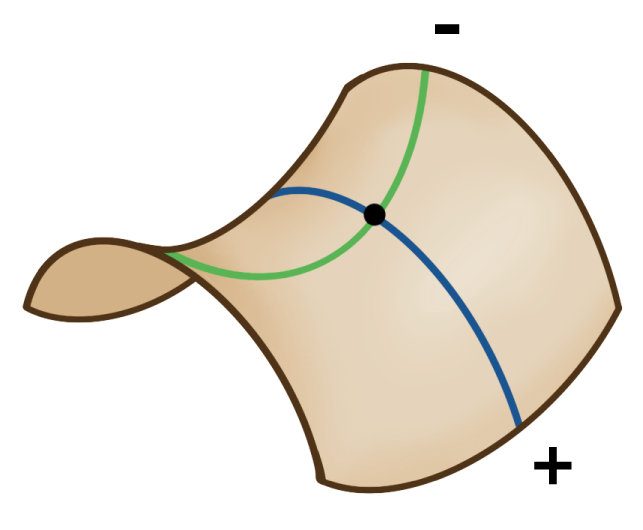 |
Figure 2 The Gaussian curvature is obtained by multiplying the maximum (blue) and minimum (green) normal curvatures at a point of a surface. The three surfaces have a (a) positive, (b) zero and (c) negative Gaussian curvatures respectively at the labelled point.
The Remarkable Theorem
Then why is Gaussian curvature important? We have to understand the “Theorema Egregrium” established by Gauss, which is Latin for “remarkable theorem”. The theorem states that the Gaussian curvature is an intrinsic measure of a surface, meaning that the Gaussian curvature at every point of the surface does not change by bending the surface, as long as you do not stretch it.
To demonstrate this idea, imagine rolling a piece of paper into a cylinder. Since a flat piece of paper has a zero Gaussian curvature everywhere (with normal curvatures being zero in all directions), by the Theorema Egregium, we know the cylinder also has a zero Gaussian curvature everywhere. And in fact, it is true as you can see in figure 3. The minimum normal curvature is always zero, so multiplying zero always gives zero.
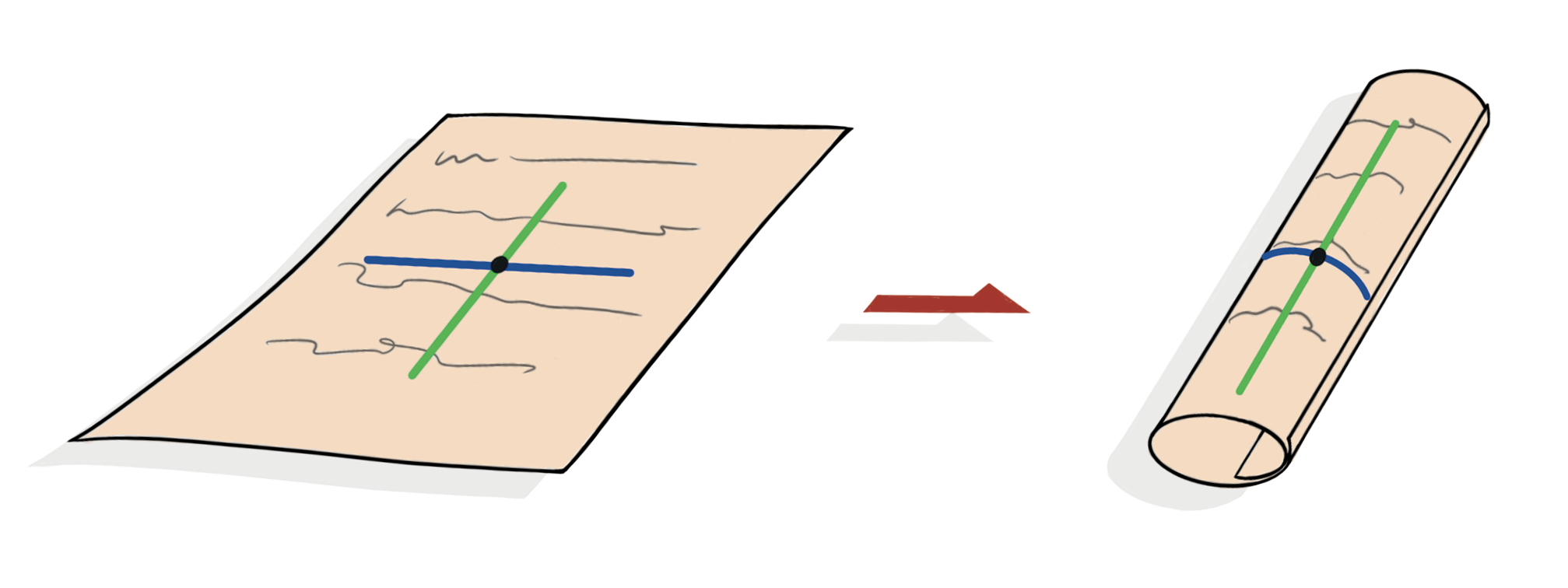
Figure 3 A flat piece of paper (left) and a cylinder resulted from rolling the paper (right). Both have a zero Gaussian curvature, with a minimum (= 0) and maximum normal curvature of the cylinder at the black dot labelled in green and blue, respectively.
A significant consequence of Theorema Egregium is that a ball cannot be completely laid flat since the Gaussian curvature of a ball is positive while a flat plane is zero. In particular, it is impossible to create a flat map of the Earth without any stretching, so the world map must be distorted to compensate for the Gaussian curvature. More interestingly, although there is no area-preserving map, there are still maps which preserve angles, such as maps on the Mercator projection (figure 4). These maps are crucial especially for marine navigation to ensure that one can reach the destination by heading to the angle shown on the map.
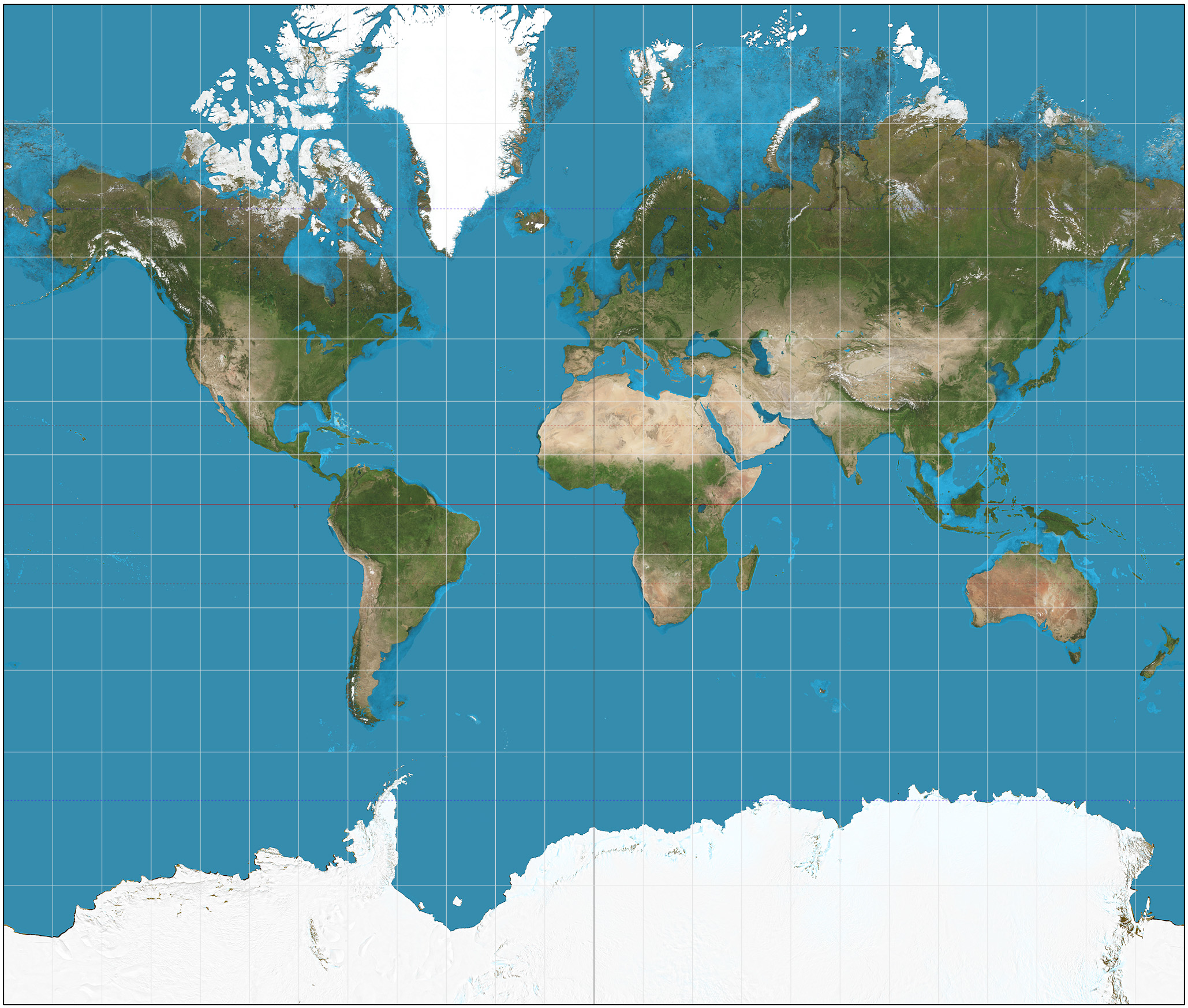
Figure 4 The world map on Mercator projection, which preserve angles but not area. Regions at high latitudes are largely distorted.
Photo credit: Daniel R. Strebe [1]
How to Eat a Pizza Decently?
Finally, we go back to the Gaussian hold of pizza. A pizza slice has a zero Gaussian curvature everywhere since the dough was rolled out flat before baking. By bending the crust to fold the pizza slice sideways and not in any other direction, we preserve a zero normal curvature everywhere of the pizza slice to maintain its zero Gaussian curvature (refer to figure 2(b) again), in a way that keeps the pizza “straight” so that the tip of the pizza can safely arrive at our lip.
Congratulations! Now you know not only how to eat a pizza elegantly, but also the reason behind the technique. This problem regarding the curvature of surfaces is in the field of differential geometry, which deals with the geometries of smooth shapes and involves mathematical techniques from calculus and linear algebra. Now try it yourself, the Gaussian hold for pizzas!
- Fun fact: By rotating the surface around the center, you should also be able to find a curve with a zero normal curvature, i.e. a straight line. Can you find it?
- Technically, there is a specific way to find out the normal curvature with respect to a certain direction, that is to create a perpendicular plane along that direction, and the normal curvature at that point is exactly the curvature of the point on the line of intersection between the plane and the surface.
- This is possible due to the extreme value theorem. Since the surface is smooth, rotating it to consider every direction is a continuous process so the normal curvature must attain a maximum and a minimum each at least one.
Reference
[1] Strebe, D. R. (2011, December 16). [The world on Mercator projection between 85°3'4"S and 85°3'4"N]. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Mercator_projection_Square.JPG