啤酒、學生與t分佈
By Helen Wong 王思齊

專題研習是否能提升學生的學業表現?哪位候選人更有可能在選舉中勝出?某種新藥對治療特定疾病是否有效?
雖然這些情境看似毫無關聯,但它們都指向一個核心概念:我們需要從樣本收集資訊,然後針對某個總體(population)作出推論,總體可以是全體學生、全體選民,也可以是全體病人。這過程被稱為「統計推論」(statistical inference)。假設抽樣過程是隨機且無偏的,從樣本中計算出的統計數值,如樣本平均值和樣本方差等,在每次取樣皆會有所不同。
因此,從多次抽樣中得到的樣本平均值會遵循一個特定的分佈。撇開嚴謹的數學證明不說,根據中心極限定理(central limit theorem),當樣本量足夠大時,即使總體並非正態分佈(normally distributed),樣本平均值的抽樣分佈(sampling distribution of the sample mean)仍會近似正態分佈。
但如果樣本量很小,且我們對總體的標準差沒有頭緒時,又該怎麼辦呢?今天我們早已習以為常:在這種情況下,只要總體為正態分佈,樣本平均值的抽樣分佈就會遵循學生t分佈(註一)。這一重要發現要歸功於一位名叫William Sealy Gosset(1876–1937)的釀酒師 [1–3]。
Gosset出生於英格蘭的坎特伯雷,1899年於牛津大學取得化學一級榮譽學位。當時,位於都柏林的健力士(Guinness)啤酒廠意識到在釀酒過程中進行嚴格品質控制的重要性,因而開始從牛津和劍橋大學招募畢業生,Gosset便是其中之一。
作為見習釀酒師,Gosset的工作是評估大麥和啤酒花的品質如何影響啤酒品質。農產品的品質會隨氣候和土壤條件等因素而有所波動,因此Gosset的目標是在確保成本效益的同時,將啤酒品質維持在高水平,這就需要從小量樣本推論出大規模的釀造過程是否合乎標準。
20世紀初已經存在中心極限定理,許多人已經熟悉在樣本數量足夠大時使用正態分佈進行統計推論。Gosset透過量度在不同條件下(例如使用不同批次的發芽大麥)釀造出來啤酒的酸度值,以判斷不同批次啤酒是否在平均酸度上存在顯著差異。
透過計算,Gosset發現當樣本量較小時,樣本平均值的抽樣分佈會明顯偏離正態分佈。這個發現促使他開始尋找類似正態分佈,但適合小樣本量的新型分佈。
雖然Gosset曾在牛津大學的數學考試中取得優秀成績,但他顯然並非專業數學家,因此學生t分佈的誕生其實有賴他與當時多位頂尖統計學家的緊密聯繫。
其中,Karl Pearson(註二)對Gosset的職業生涯影響深遠。Pearson向Gosset介紹了幾乎所有當時已知的統計方法,並邀請他於1906至1907年訪問Pearson於倫敦大學學院所在的學系。在此期間,Gosset專注研究小樣本問題,並於 1908 年在Pearson主編的《Biometrika》期刊上發表了一篇劃時代的論文〈平均值的可能誤差〉(The Probable Error of a Mean)[4]。
細心的讀者或許會注意到,這篇論文的作者署名是「Student」(學生),而非Gosset的本名。這是因為健力士啤酒廠有一項規定,禁止員工以本名或使用任何公司數據發表論文。為了遵守這項政策,Gosset選擇使用筆名「Student」發表論文,據說靈感來自他當時使用的筆記本封面標題《學生的科學筆記本》(The Student’s Science Notebook)[5]。
然而,「t分佈」這個名稱並非出自Gosset本人。在1908年的論文中,Gosset仍然使用符號z來推導樣本量為4到10時樣本平均值的抽樣分佈。符號t稍後由傳奇統計學家兼Gosset好友Ronald Fisher(註三)於1925 年的論文引入 [6]。Fisher在這篇著作中完整推導出學生t分佈的值,並證明了它是一種經轉換後的正態分佈。t分佈的形狀會隨樣本量n改變,而技術上樣本量會以自由度(degree of freedom,即n – 1)表示。在樣本量較小的情況下,相比起正態分佈,t分佈的峰部會較矮,尾部也較「粗」(圖一)。隨著樣本量增加,尤其當n大於 30 時,t分佈會開始變得接近正態分佈。
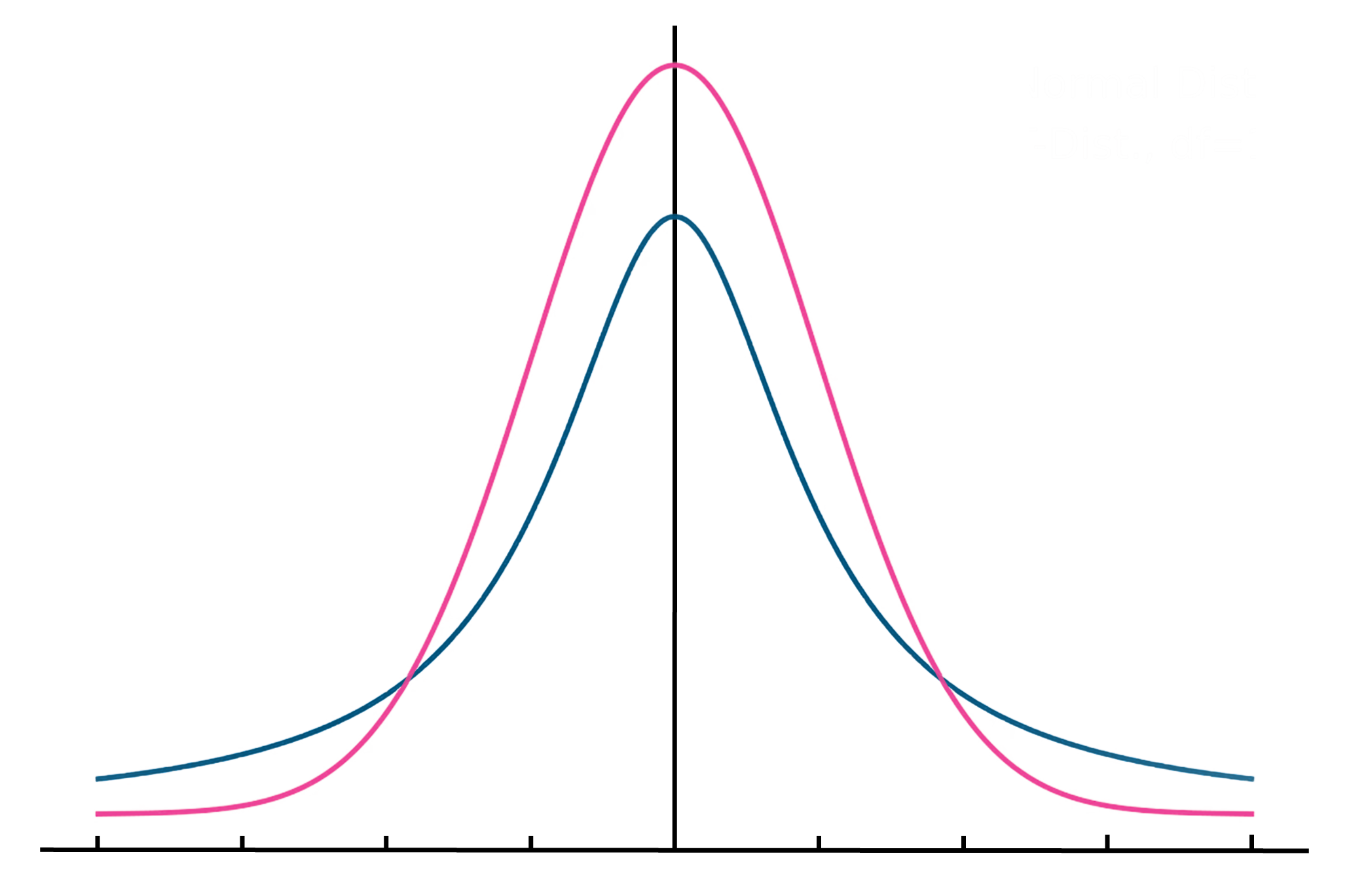
圖一 正態分佈(粉紅)和自由度為1時的t分佈(藍)。與正態分佈相比,t分佈的峰部較矮,尾部較「粗」。
Gosset自己曾在寫給Fisher的信中評論道:「你很可能是唯一一個會用這些東西的人!」然而,讓Gosset始料不及的是t分佈如今已成為最著名的統計分佈之一。它被廣泛應用於日常生活和學術研究中,更不必說在統計學課程中可以經常找到它的蹤影。因此,下次當你在遇到學生t分佈,或在課堂中被它搞得頭昏腦脹時,別忘了那位真正的「學生」— William Sealy Gosset,以及背後的精彩故事。
註腳
編按:學生t分佈(Student’s t-distribution)有時會根據讀音被翻譯成「司徒頓t分佈」。
Karl Pearson(1857–1936)是英國統計學家,也是推動現代統計學發展的關鍵人物 [7]。他的工作為許多至今仍被廣泛使用的統計方法和概念奠定了基礎,包括Pearson相關係數和卡方分佈。值得一提的是,Pearson於1911年在倫敦大學學院成立了全世界第一個統計學系。
- Ronald Aylmer Fisher(1890–1962)是英國統計學和遺傳學家 [8]。Fisher被譽為「幾乎以一己之力奠定現代統計科學基礎的天才」,他對統計學的貢獻包括顯著性檢驗、變異數分析(ANOVA)和最大似然估計等。在遺傳學方面,他被視為群體遺傳學的三位奠基人之一。群體遺傳學是結合孟德爾遺傳學和達爾文演化論的現代演化綜論(modern synthesis)的重要組成部分。
參考資料
[1] Brown, A. (2008). The strange origins of the Student’s t-test. Physiology News, Summer 2008, 13–16. https://doi.org/10.36866/pn.71.13
[2] Pearson, E. S., Gosset, W. S., Plackett, R. L., & Barnard, G. A. (1990). Student: A statistical biography of William Sealy Gosset. Clarendon Press; Oxford University Press.
[3] Trkulja, V., & Hrabač, P. (2020). The role of t test in beer brewing. Croatian Medical Journal, 61(1), 69–72. https://doi.org/10.3325/cmj.2020.61.69
[4] Student. (1908). The Probable Error of a Mean. Biometrika, 6(1), 1. https://doi.org/10.2307/2331554
[5] Ziliak, S. T. (2008). Retrospectives: Guinnessometrics: The Economic Foundation of “Student’s” t. Journal of Economic Perspectives, 22(4), 199–216. https://doi.org/10.1257/jep.22.4.199
[6] Fisher, R. A. (1925). Applications of Student’s distribution. Metron, 5, 90–104.
[7] Magnello, M. E. (2014). Pearson, Karl: His Life and Contribution to Statistics. In Wiley StatsRef: Statistics Reference Online. John Wiley & Sons, Ltd. https://doi.org/10.1002/9781118445112.stat04822
[8] UCL. (2021, March 2). Ronald Aylmer Fisher (1890-1962). https://www.ucl.ac.uk/biosciences/gee/ucl-centre-computational-biology/ronald-aylmer-fisher-1890-1962