Piet Hein：「在文明社會的圖樣中有著兩種傾向，一種是直線和矩形，另一種是曲線。無論在機械或心理上，我們都有原因解釋這兩種傾向：直線構成的物件能被整齊地放在一起，節省空間；我們亦可以 — 物理或心理上 — 輕鬆地移動由曲線構成的東西。然而我們彷彿被束縛著一樣被迫二擇其一，但有時採取兩者之間的形態卻會更好 [1]。」

畫一條線，隨意畫，你會發現那條線只能是直線或曲線。把一條曲線延長，到某個位置它會閉合成圓。使兩條直線相交，你會得到一隻角；把角度調得工整一點，你就會得一隻直角。曲與直就像無處不在的兩股勢力，而在它們崛起的同時數學家就已經著手研究兩者的差異。世上最著名、歷久不衰的幾何教科書 — 歐幾里得的《幾何原本》在起首正是假設我們無論如何都能畫出直線、直角和圓形。笛卡兒在代數以現代形式出現後僅僅約一世紀，就提出了把幾何圖形和問題轉化為代數的概念，統整了數學上這兩個主要範疇。這亦是今天學校仍會教授笛卡兒坐標圖（就是以我們大家都熟識的坐標系統所畫的圖）的原因。

在慣常的x-y平面上，直線的方程就是我們熟識的y = mx + c。線性方程，即是最高次項為x或y的方程永遠會得出一條直線；二次方程，即是最高次項為x²或y²的方程則會得出其中一種圓錐曲線 — 圓形、橢圓、拋物線或雙曲線 [1]。如果我們考慮橢圓的方程x²/a² + y²/b² = 1，當a = b時就會變成大家都熟知的圓方程x² + y² = 1。在1818年，這全都是數學家已知的事實。在一本於當年出版的幾何書籍裡，Gabriel Lamé決定再進一步看看如果指數n變成2以外的值時會發生甚麼事 [2]。

方程xⁿ + yⁿ = 1的曲線可以根據n被分成不同種類 [3]，但當中最有趣的是當n為分數p/q，且p為偶數，q為奇數而且大於1時的曲線，這些分數包含了2、4、6、8在內的所有偶整數。

隨n增加成更大的偶整數，你可以看到圖形由n = 2時的圓形變得越來越接近一個正方形（圖一）。透過取絕對值，我們允許n為任何數；現在的Lamé曲線 |x|ⁿ + |y|ⁿ = 1在n > 2的情況下，由n = 2時的圓形連續地變成n趨向無限大極限時的正方形。Lamé曲線的一般方程 |x/a|ⁿ + |y/b|ⁿ = 1也是如此，取相同極限時會變成矩形。如果你從未聽過正方形或長方形方程的話，恭喜你，你現在知道了！

圖一  n增加時Lamé曲線的轉變（左至右分別為n = 2和n = 4）

感謝繪圖工具和代數提供的簡潔表達，我們現在擁有可以被簡單描述，一個介乎正方形和圓形之間的圖形。簡潔正是令這條形狀曖昧的曲線突然被再次提起，並被採用於多個意想不到的情境中的原因。以下是幾個例子。

在1959年，瑞典建築師想在斯德哥爾摩市中心被建築物包圍的長方形用地興建一座迴旋處 [4]。迴旋處當然多數都以圓形設計，但圓形會浪費大部分用地；使用橢圓形的話，兩端的急彎會造成駕駛上的不便。城市規劃師也提出過以八條弧組成環形的方案，不過這會使車輛轉過多不必要的彎。後來這道難題成為了設計比賽的題目，引起了丹麥設計師及科學家Piet Hein的注意。大會藉著他的數學背景找到了這個橢圓形與矩形之間的折衷辦法。Piet Hein無意中發現Lamé曲線，他嘗試把不同數值代入n去改造一個寬度為6和高度為5（即a = 6、b = 5）的橢圓形，最後決定採用n = 5/2或2.5（圖二）[5]，並稱這個圖形為「超橢圓」。

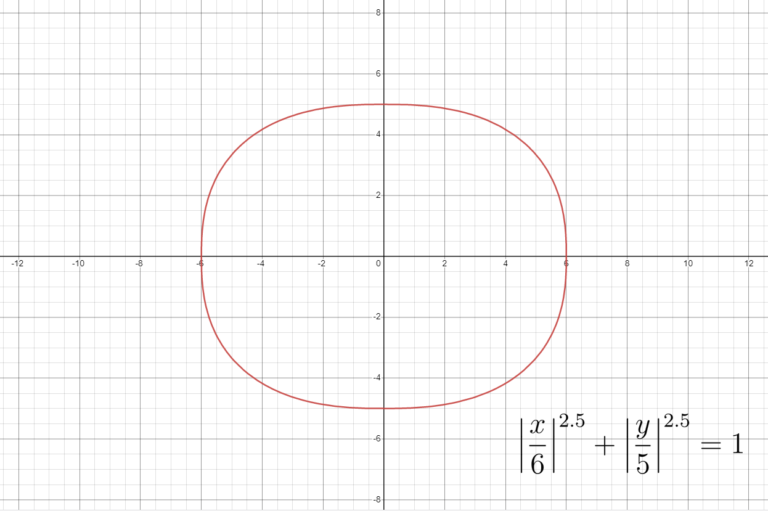
圖二  Piet Hein提出的斯德哥爾摩迴旋處方案

Piet Hein認為這個形狀是最美麗而又可行的解決方案。在隨後一篇文章，他這樣寫道[1]：

「徒手畫些東西的話 — 像是他們［其他建築師］為斯德哥爾摩迴旋處所畫，由不同形狀拼湊而成的圖形 — 並行不通。那樣的圖形並不規則，也不像圓形或方形般有明確的定義；你既不知道那是甚麼，那亦毫不美觀。超橢圓就能解決這個問題，它不圓也不方，介乎兩者之間，但它既是個規則的圖形，也有明確的定義 — 它有種統一性。」

在iOS 6升級iOS 7的時候，蘋果的設計部門也決定採用這個美觀的圖形。在那之前iOS應用程式的圖示都是在正方形加上圓角（圖三）[6]，這與斯德哥爾摩迴旋處問題同出一轍：直線至圓形之間過於兀突的過渡會在不經意間為我們帶來視覺上的不快。

因此蘋果的設計師基於Lamé曲線設計出新的應用程式圖示。他們採用了n = 26/5或5.2的曲線再加上少許改動 [7]，使圖形有著流暢而更自然的外型。（要注意即使n是如5.2般較大的數字，超橢圓的四邊都不是直線，而是曲線。）

圖三  iOS 6（正方形加上圓角）及iOS 7+（作過改動的超橢圓）上的應用程式圖示

小米也許有著相同的想法。在2021年，小米把公司標誌由帶圓角的正方形改為明顯是Lamé曲線的圖形（圖四）。

圖四  小米新舊標誌的形狀（左邊為舊標誌，右邊為新標誌）

首屈一指的日本設計師原研哉監督了整個計劃，他的做法跟Piet Hein一樣，但認為n = 3才最為美觀 [8]。然而Piet Hein跟小米的故事又有著不同之處：Piet Hein選用超橢圓是有他明確的原因，但小米據報支付了原研哉二百萬元人民幣，對方就只對公司標誌的形狀作出了這項小改動，而沒有別的大改變。網民一致認為這次重新設計標誌並沒有任何意義 [9]，皆因小米早已有具標誌性的公司標誌。那重新設計真的有其意義嗎？根據原研哉的說法，答案是有意義的，因為新標誌是「小米內在精神的象徵」，以及是「對『Alive』（生命感）這個設計概念的呼應 [8]」。

Lamé曲線是曲和直之間的折衷點，也是在漫無目的的好奇下誕生的有用工具。大部分的數學也是如此：它可能隱沒在人們的視線外，可能用上200年才找到它的用途，偶爾也可能成為網民訕笑的對象；但如果你懂得怎去發掘，它就在那裡。

參考資料：

[1] Bellos, A. (2010). Alex’s Adventures in Numberland. Bloomsbury.

[2] Lamé, G. (1818). Examen des différentes méthodes employées pour résoudre les problèmes de géométrie [Examination of the different methods to solve geometry problems]. Vve Courcier. https://gallica.bnf.fr/ark:/12148/bpt6k92728m/f119.item

[3] Jaklič, A., Leonardis, A., & Solina, F. (2000). Segmentation and Recovery of Superquadrics. Springer.

[4] Gardner, M. (1965). The superellipse: a curve that lies between the ellipse and the rectangle. Scientific American, 213(3), 222-238. https://www.jstor.org/stable/10.2307/24931123

[5] Gridgeman, N. T. (1970). Lamé Ovals. Mathematical Gazette, 54(387), 31-37. https://doi.org/10.2307/3613154

[6] Mynttinen, I. (2020, October 18). The iOS Design Guidelines. https://ivomynttinen.com/blog/ios-design-guidelines

[7] Rosenfeld, L. (2021, October 12). My quest for the Apple icon shape. https://liamrosenfeld.com/posts/apple_icon_quest/

[8] Vincent, J. (2021, March 30). Xiaomi’s new logo is almost unrecognizable. The Verge. https://www.theverge.com/tech/2021/3/30/22358033/xiaomi-new-logo-design-square-round

[9] Shen, X. (2021, April 2). Xiaomi’s new ‘squircle’ logo becomes the butt of online jokes with many claiming they could have made it for much less money. South China Morning Post. https://www.scmp.com/tech/big-tech/article/3127984/xiaomis-new-squircle-logo-becomes-butt-online-jokes-many-claiming