如何不失禮地吃薄餅?
By Devandhira Wijaya Wangsa

薄餅慘劇
如果你現在要吃一塊薄餅,你會怎樣做?通常事情會這樣發生:
- 你握住薄餅邊緣。
- 薄餅從你手中垂下,來回搖晃。
- 配料掉到桌上,你無奈地坐在那裡,看著桌子變成一團糟!
自薄餅誕生多個世紀以來,這一直都是我們吃薄餅的悲慘宿命。然而,你只要從批邊將薄餅沿長邊對折,就能使薄餅保持筆直,然後輕鬆地吃掉薄餅。姑且讓筆者稱這個方法為「高斯握法」,靈感來自數學家卡爾.弗里德里希.高斯(Carl Friedrich Gauss)!
從數學角度看,這個秘技與一個叫曲率的概念有關。曲率的概念對我們來說並不陌生,它是衡量「彎曲」程度的一個值。對於一維曲線,曲線在某一點上越為彎曲,其曲率就越大。從數字上量化的話,一個半徑為 r 的圓在每一點上的曲率均為1/r,因此大圓的「彎曲程度」比小圓要小。那很自然地,直線上任何點的曲率皆為零,即是沒有彎曲。此處要注意的是描述某一點的曲率是較為可取的做法,因為曲線在不同點上可以有不同的曲率。
然而,在我們原本的問題中,我們處理的是一個表面(嚴格來說,因為薄餅有厚度,所以並不是一個表面,但我們可以暫且將其視為一個表面)。那麼,曲率的概念如何與屈曲表面的法則相關呢?須知道有種曲率叫「高斯曲率」,答案就在於一個與其相關的絕妙結果。
高斯曲率
讓我們討論如何描述一個表面的曲率。試想像一個三維物體的表面,譬如紙張、球體、圓柱體、品客薯片,甚或是甜甜圈。對於表面上的某一點,你會發現曲率會根據所考慮的表面方向而有所不同。更具體的例子請看圖一的表面,試找出圖表中心點(原點)的曲率。
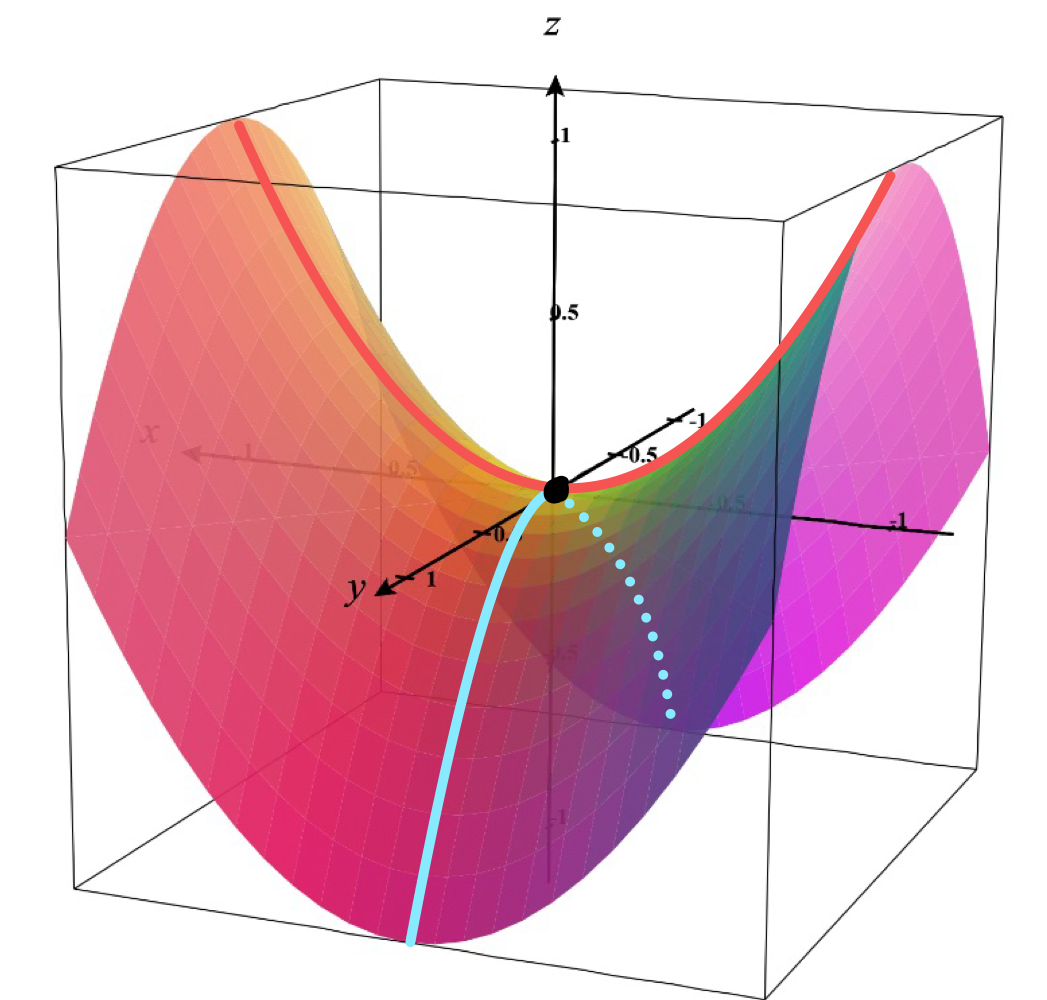
圖一 一個在中心點(原點)同時具有正(紅)和負(藍)法曲率的表面(註一)。
根據我們所考慮的表面方向(紅或藍),我們會得出不同曲率:紅色曲線兩側向上彎,而藍色曲線兩側向下彎。這麼,在中心點上,我們可以說紅色曲線具有正曲率,而藍色曲線具有負曲率(正負純粹取決於慣用定義)。此處要注意的是即使這些曲線跨越整個表面,但我們只考慮中心點的曲率。
我們稱之為「法曲率」— 即是在考慮穿過該點的某曲線下,一個表面在該點的曲率(註二)。在我們的例子中,該表面在朝紅色曲線的方向上具有正法曲率,而在朝藍色曲線的方向上具有負法曲率。
現在想像一下,我們透過繪畫朝向每個可能方向的所有曲線,來考慮某一點上的所有可能法曲率。在這些可能性中,必然存在最大和最小法曲率(註三),將這兩個曲率相乘便能得出高斯曲率。
讓我們看看圖二的三個例子。第一個表面在標記點上具有正高斯曲率,因為最大和最小法曲率皆為正數,因此它們的乘積也是正數。以相同道理推敲,可以得知其餘兩個形狀分別具有零和負的高斯曲率。儘管還有其他方法可以描述某一點上的表面曲率,例如平均曲率等,但只有高斯曲率與我們的問題相關。
(甲) 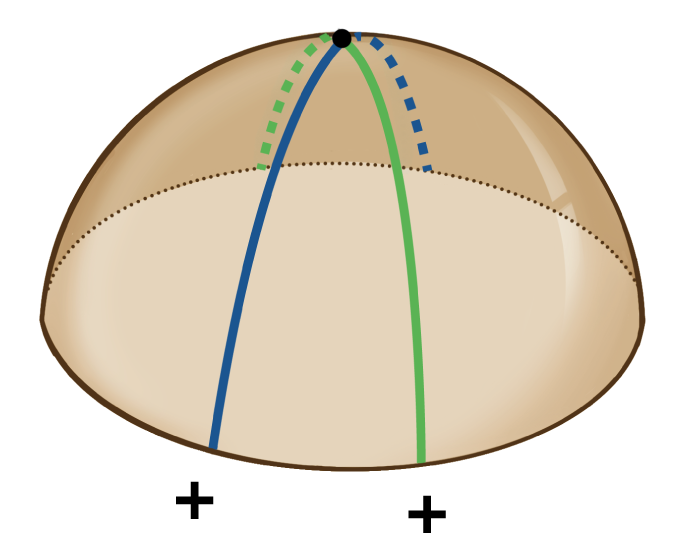 | (乙) 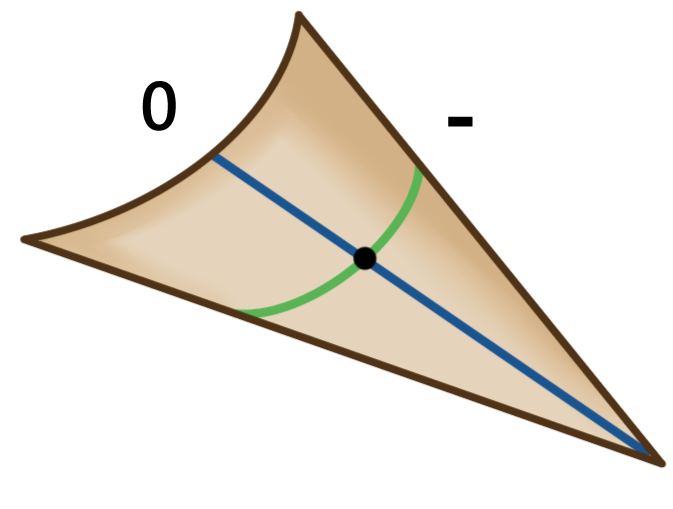 | (丙) 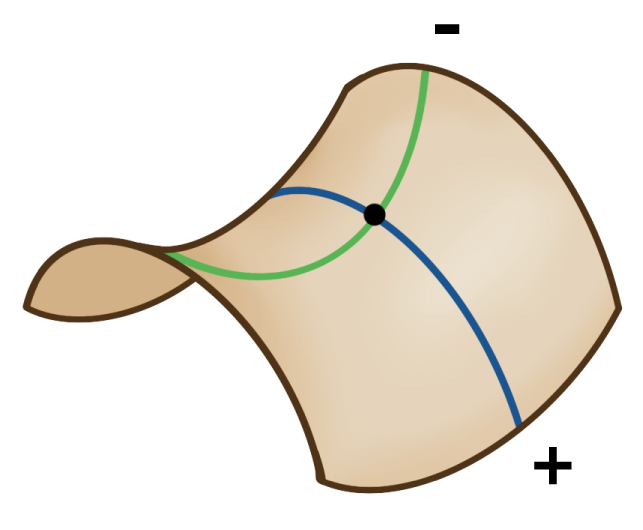 |
圖二 高斯曲率是透過將表面上某一點的最大(藍)和最小(綠)法曲率相乘所得。圖中三個表面在標記點上分別具有(甲)正、(乙)零和(丙)負高斯曲率。
絕妙定理
那麼,為甚麼高斯曲率重要呢?我們必須了解高斯所提出的「Theorema Egregium」,這在拉丁語中解作「絕妙定理」(remarkable theorem)。該定理指出,高斯曲率是一個表面的內在本質,意味著只要不把表面拉長,單單屈曲表面是不會令表面上每一點的高斯曲率改變。
為了理解這個概念,試想像將一張紙卷成圓柱狀。由於在平坦紙張上各處的高斯曲率都是零(所有方向的法曲率均為零),根據絕妙定理,我們知道圓柱上每一點的高斯曲率也是零。事實上正如圖三所示,確實如此,因為每一點的最小法曲率均是零,因此乘以零得出的積亦是零。
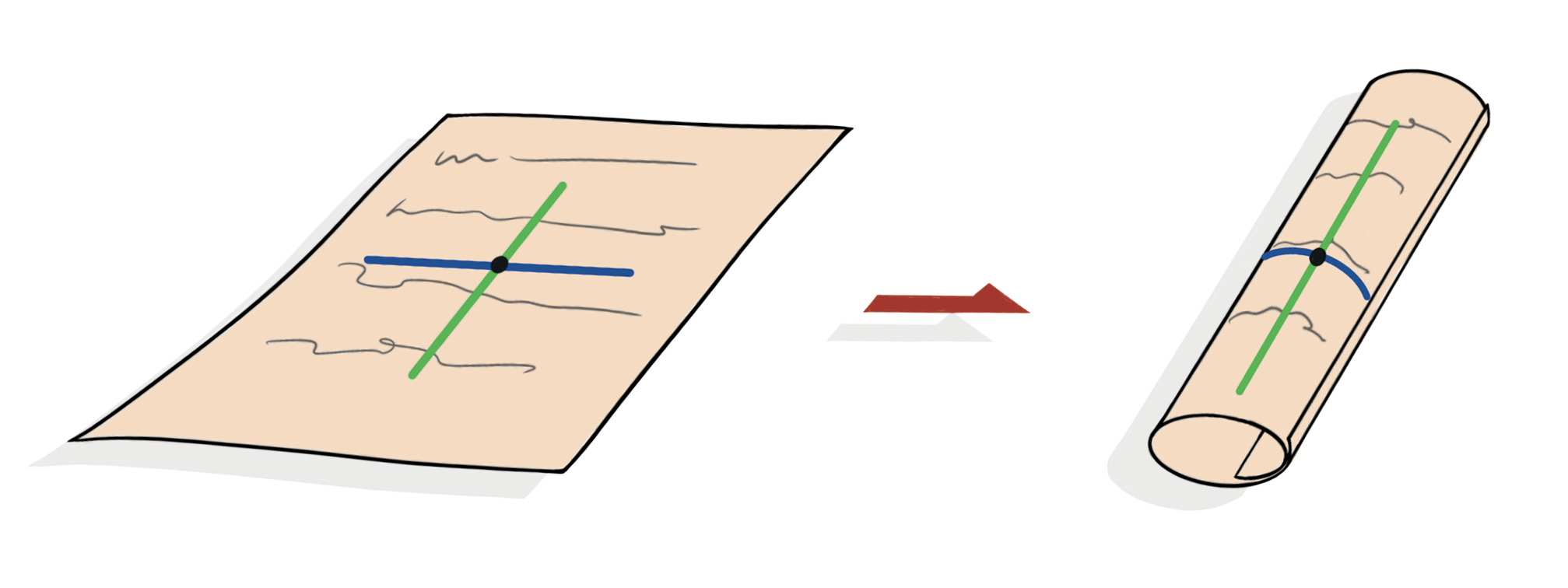
圖三 扁平的紙張(左)和由其卷成的圓柱(右)。兩者的高斯曲率均為零,圓柱在標記點上的最小(= 0)和最大法曲率分別以綠色和藍色表示。
絕妙定理帶來的重要啟示是球體無法被完全攤平,因為球體的高斯曲率為正,而平面的為零,所以我們無法在沒有「拉伸」的情況下建立平面的世界地圖,故此世界地圖必須失真以補償高斯曲率。更有趣的是,儘管沒有地圖能按實際面積比例繪畫所有國家,但我們仍能編製出方位正確的地圖,例如以麥卡托投影法(Mercator projection)製作的地圖(註四)。這種地圖對航海等用途至關重要,因為它能確保人們按照地圖上顯示的角度行駛就能到達目的地。
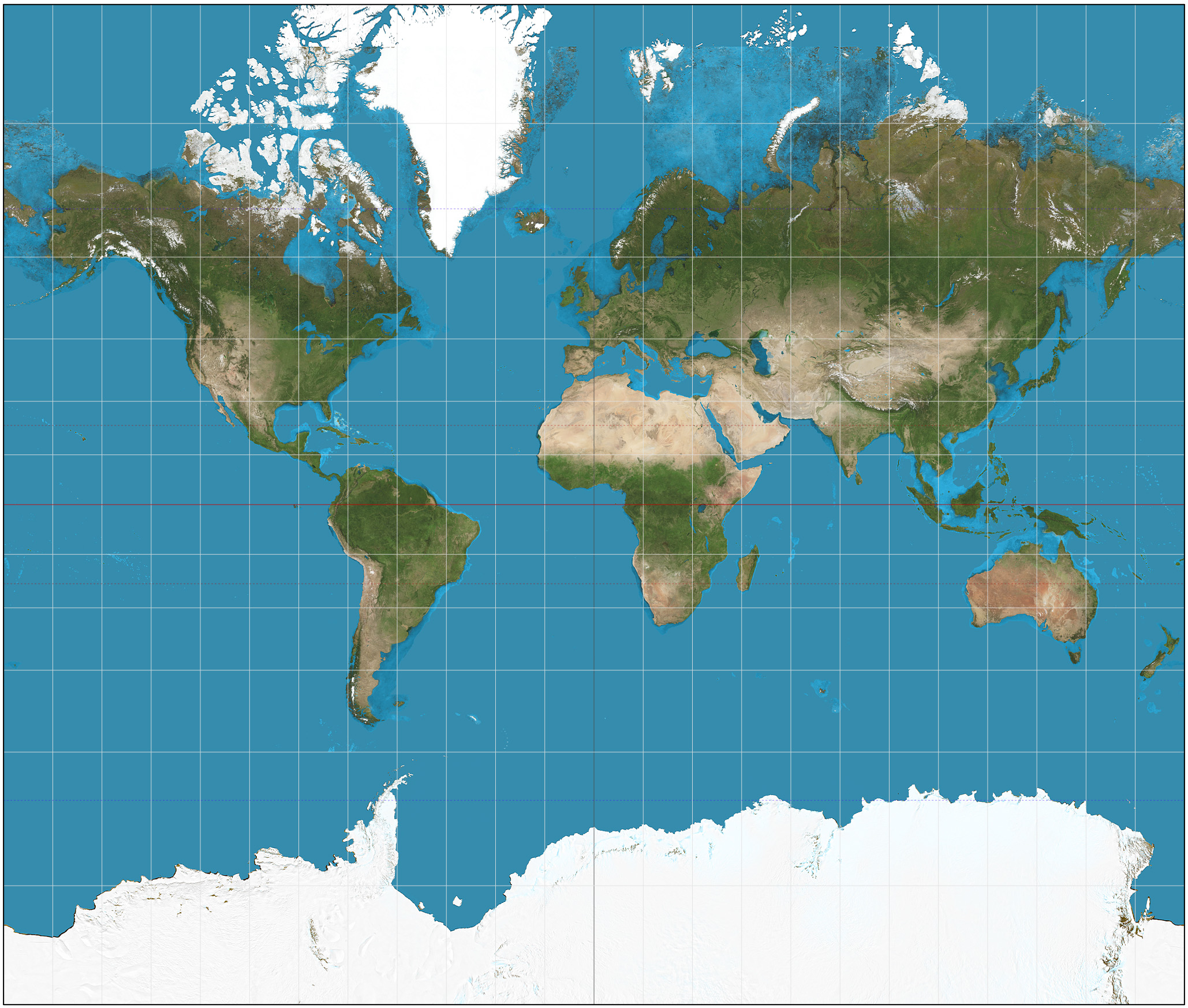
圖四 以麥卡托投影法編製的世界地圖。它能保留實際角度,但不反映實際面積,明顯地高緯度地區嚴重變形。
圖片來源:Daniel R. Strebe [1]
如何不失禮地吃薄餅?
最後回到我們吃薄餅的高斯握法。由麵團在烤焗前被擀平的一刻,薄餅每一點的高斯曲率均注定為零。透過屈曲批邊將薄餅沿長邊折疊,而不是沿其他方向,我們就能保持薄餅在每一點上均有零法曲率來維持其零高斯曲率(再次參考圖二),使薄餅能穩定地沿長邊挺直,令薄餅的尖端能安全抵達到我們的嘴巴。
恭喜!現在你不僅知道如何優雅地吃薄餅,還知道背後的原理。這個關於表面曲率的問題屬於微分幾何的範疇,該範疇探討光滑形狀的幾何,並涉及微積分和線性代數上的數學技巧。事不宜遲,就試用高斯握法吃薄餅吧!
- 知多一點點:透過圍繞中心旋轉表面,你應該能找到一條法曲率為零的曲線,亦即是一條直線。你能找到嗎?
- 事實上,有更嚴謹的方法找出相對於某一方向的法曲率,那需要沿該方向建立一個垂直平面,該點的法曲率正是垂直平面與表面相交線上該點的曲率。
- 這是由於極值定理(extreme value theorem),因為旋轉光滑表面以考慮每個方向是一個連續過程,因此法曲率必定會達到最大值和最小值各至少一次。
參考資料
[1] Strebe, D. R. (2011, December 16). [The world on Mercator projection between 85°3'4"S and 85°3'4"N]. Wikimedia Commons. https://commons.wikimedia.org/wiki/File:Mercator_projection_Square.JPG