我們居住的世界浩瀚無垠 — 遼闊的陸地和海洋，亦只是宇宙的一小部分。透過嘗試理解我們所身處的世界，對人類而言是一種在未知中的慰藉。我們透過從事物中找出規律來認識世界，黃金比例就是其中一個例子。

在數學上，黃金比例以希臘字母φ表示。它是一個無理數，與π一樣有著無限個小數位，並且不能被表達成兩個整數之比。在歷史長河中，黃金比例這個無理數吸引了世界上不少數學家、生物學家、藝術家和建築師的目光 [1]。你或許現在就想知道黃金比例究竟是甚麼，以及它為何如此獨特；在搞清楚這一切之前，讓我們先設x為一線段的長度，然後把這線段一分為二，當中一段比另一段長。如圖一所示，設較長一段的長度為1，而餘下部分為x – 1。

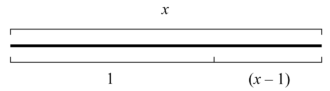
圖一　把長度為x的線段分成兩部分

那麼，如果x與較長一段之比和較長一段與較短一段之比相同，前者之比需為甚麼？

​

要找出這個「神聖比例」x的值，我們可以藉上述關係推導出一條二元方程。

​

透過解方程並捨去負數解後，我們可以得出x等於 ，大約是1.618 － 這就是黃金比例的值。你可能聽過另一個與黃金比例相關的著名數學概念 － 斐波那契數（Fibonacci numbers (F_n)），數列中的每個數均為其前兩者之和：0, 1, 1, 2, 3, 5……聰明的你也許已經察覺到，每個斐波那契數與數列中前一個數之比的極限（limit）正是黃金比例φ。換言之，隨著數列中的數字越來越大，前後兩者之比會越接近φ。

人們經常把φ與美學扯上關係，稱之為「比例之美」[2]。φ出現在大自然的不同領域中，還據說在過去數千年啟發了不少藝術家和建築師。譬如說某些植物的葉序（葉片圍繞莖部生長的排列形態）與黃金分割相關，在相鄰葉片或葉片對之間的角度可以呈90度（稱為十字或交互形態）或180度（二列形態）的同時，螺旋葉序也是在植物中非常普遍的，當中相鄰葉片或葉片對的角度是與黃金角度接近的137.5度（註一；圖二）[3]。不難想像我們在大自然中一次又一次地與這個比例的相遇，大概已經勾起古希臘人和我們對它的興趣和敬畏之情，這從巴特農神殿的建築融合了黃金比例和達文西的〈最後的晚餐〉中就能看到端倪 [1]。黃金比例接二連三出地現在不同作品中，使人不禁問道：在人類追求美感的探索中，黃金比例真的是構成美的其中一個的因素嗎？

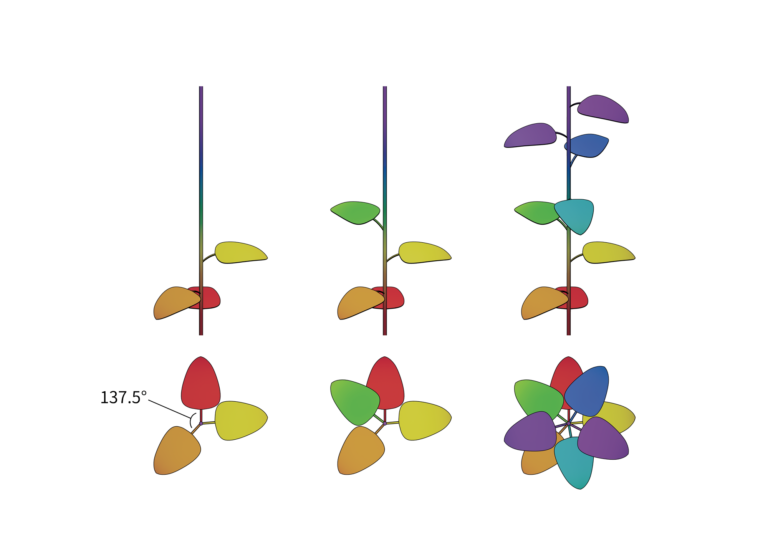
圖二　螺旋葉序（低至高的葉片依次以紅至紫的「假色（pseudo color）」表示。）

令人意外的是，這也許只是我們一廂情願，是過分猜想令我們認為它在大自然中無所不在。人類腦袋天生喜愛尋找規律，喜愛得即使沒有實質證據支持也寧願相信φ出現不同情境中 [1]。關於這個誤會最具說服力的例子是鸚鵡螺外殼的外觀。

鸚鵡螺是一種海洋生物，與魷魚和八爪魚都屬於頭足綱的動物。與其他頭足綱動物不同，鸚鵡螺居住在分成多個腔室的漂亮螺旋外殼中。牠們外殼的螺旋曲線被稱為對數螺線或成長螺線，就是如圖三所示不斷從最內層曲線向外成長的螺旋。

圖三　鸚鵡螺的對數螺線

鸚鵡螺外殼對數螺線的長闊比被認為與黃金比例相符，因此亦被公認是自然界中出現φ的著名例子。人們之所以會有這個根深蒂固的概念，要多得包括Dan Brown的《達文西密碼》等文學作品及史密森尼學會（The Smithsonian Institution；註二）等學術機構和其他知名科學家錯誤地宣揚這件「事實」[2]。

然而，如果你有機會親身檢視鸚鵡螺外殼，你會發現它的長闊比與其說是接近φ (1.618)，其實更接近4:3 (1.333)。如果再一次認真思考「每個鸚鵡螺外殼都符合黃金比例」這個流言的話，你不覺得世間上所有鸚鵡螺外殼都擁有一模一樣比例的想法有點奇怪嗎？相反，如果每個樣本之間都有著些微差異，即使是小數點後數個位也好，這不是會更為合理嗎？

這正是一位名叫Christopher Bartlett的研究員所抱持的想法，他甚至推測4:3也不能準確地描述大多數鸚鵡螺外殼的比例。在檢查史密森尼學會館藏的80個外殼後，他最終發現平均比例是1.310。另外，全部外殼的比例都有著些微差異，因此所有外殼均擁有1.6之類相同比例的說法顯然是錯的，而1.310本身也比1.6離φ的準確值更遠 [2]。

那為甚麼有這麼多科學家和教育工作者相信這個流言呢？嗯，像前面提到的一樣，人類的生存之道以及對自然萬物之理的詮釋一向有賴觀察規律，有時潛意識對尋找規律的固執會勝過我們的理性判斷，以致出現黃金比例無處不在等的美麗錯覺；然而，人性的另一個優點是我們有著無窮的好奇心，使我們不但能創造流言，亦能破解流言。

1 黃金角度：假設我們要把一個圓形以黃金比例分成兩個扇形，在設大小扇形的圓心角分別為x和 (360 – x)度後，便可以設一道二元方程。解方程後會得出黃金角度x約為137.5度。

2 史密森尼學會：集博物館、教育及研究機構於一身，位處美國華盛頓特區的大型綜合學術組織。

參考資料：

[1] Iosa, M., Morone, G., & Paolucci, S. (2018). Phi in physiology, Psychology and Biomechanics: The golden ratio between myth and science. BioSystems, 165, 31–39. doi:10.1016/j.biosystems.2018.01.001

[2] Bartlett, C. (2018). Nautilus Spirals and the Meta-Golden Ratio Chi. Nexus Network Journal, 21, 641–656. https://doi.org/10.1007/s00004-018-0419-3

[3] Strauss, S., Lempe, J., Prusinkiewicz, P., Tsiantis, M., & Smith, R. S. (2020). Phyllotaxis: is the golden angle optimal for light capture?. The New Phytologist, 225(1), 499–510. doi:10.1111/nph.16040